2008.11.22(sat)
公開シンポジウム「竹の造形・その未来」6

日詰氏:
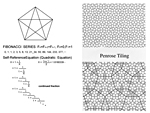
会場の前の卓上に置いてある作品群は全て黄金比が関係しています。フィボナッチ数列、ペンローズ・タイルも関係しています。今お見せしている作品「五勾(ごまがり)」は1990年に特許申請をしたものです。一見、何の変哲もないザルに思われるかもしれません。ですがペンローズ・タイルをベースに編んでいるもので、歴史上、このように編んだ人はいなかったはずです。このザルを三度笠がわりに世界中を講演旅行していますが、この編み方に気付いて声をかけられることは、まずありません。ですがバリ島では違いました。飛行機を降りた瞬間に、空港の職員に声をかけられたのです。いかにバリの人々が新しいものに対する審美眼を備えているか示しているようにも思えます。「五勾」が準周期性を平面組織に導入したものであるのに対して、隣にある「六勾(むまがり)」はそれを空間組織にまで発展させたものです。前者は二次元、後者は三次元の構造物となっています。両者の違いは次元の違いだけで、性質は全く同じです。どちらも、六次元空間の同一の構造物の影の形であり、「六勾」は六次元空間格子の三次元への投影です。

他にも副産物が色々あります。具体的な作品の説明はこの程度にして、これからは写真を中心に進めていきます。
始めに宮崎興二先生の『多面体と建築』(1979年)という本をご紹介します。この本で僕はR.バックミンスター・フラーと出会い、数式が出てこない「かたちの数学」があることに驚きました。他にもペンローズ・タイルが登場してきます。この本との出会いから僕は独自にフィボナッチ数、ペンローズ・タイル、黄金比に照準を合わせた研究を独学で始めました。1983年の頃です。もう一つ挙げておきたいのがルドルフ・シュタイナーの『新しい建築様式への道』です。僕は建築に絶望していたのですが、この本によって本当の建築の可能性に気付くことができました。この2冊が僕の原点です。
なぜ建築に絶望していたかと言いますと、僕が学生だった頃は四角い箱の集合のような建築が良いとされていたからです。そのことにどうも馴染めずにいました。そんな中、バーナード・ルドフスキーという人の『建築家なしの建築』に収められているような、数々の集落などに出会い魅了されていきました。それまで自然界の造形には魅せられていたのですが、人間がつくったものにもすごいものはあるということに気付いたのです。そこで僕もそういった集落を設計しようと思ったのですが中々うまくいかず、ジレンマを抱えていました。また同様に、音楽に関しても西洋音楽の典型的なクラシックやポップスといったものにも物足りなさを感じ、民族音楽へと魅かれており、一部、実験的な現代音楽の中にも面白さを感じていました。

そのような頃にペンローズ・タイルに出会ったのです。これで、人間が長年かけてつくりだした先ほどの集落に近いものができるのではないか、少なくとも今の建築よりはましなものができるのではないかという直観を得ました。それから10年程、ペンローズ・タイル、フィボナッチ数列、黄金比などの研究を続けました。黄金比というのは正五角形の辺と対角線の比や、フィボナッチ数列の極限項比、最も単純な2次方程式の解で得られることは良く知られています。2次方程式は自己言及的な構文とみなすことができ、黄金比は最もシンプルなフラクタル構造と位置づけられます。二次元図形であるペンローズ・タイルも同様の自己相似構造をもっています。
ここで一つ断っておかなければならないことに、世間で黄金比というと煙たがられることが多いのですが、それはピラミッドやDNA、巻貝のかたちなどに黄金比が採用されているなどといった言説が多いからなのです。それらは迷信に近く、本当の科学者であれば認めないと思いますし、僕もそういったものとは一線を画したいと思っています。なぜなら、そのような文脈で語られる黄金比においては、決して機能について言及されることはなく、かたちの美しさに終始してしまいがちですし、そもそも説得力に欠けるのです。ただし、例外としてステルス戦闘機と爆撃機は迷信ではありません。これは人間の悲しい性でしょうが、人間は新しい技術をまずろくなことに使わないですね。
それに対して植物は数千万年前から黄金比を厳密且つ平和的に活用しています。具体的には、葉のつき方が有名です。葉は、360度を黄金比で割った角度分ずれて付いているので、どの葉の上にも葉が重ならず光を受けることができ、また、植物が高層化を図った際にバランスよく直立することができているのです。こういうことこそ黄金比の使い道として学ぶべきことではないでしょうか。ステルス戦闘機とは大きく違いますよね。

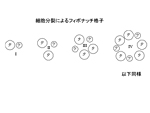
フィボナッチ数列の原理を考えるときに細胞分裂として捉えると、次のように説明できます。一つの細胞は分裂する際にメジャーとマイナーに分かれます。そしてメジャーだったものが更にメジャーとマイナーに分割され、それまでマイナーだったものがメジャーになります。この規則でどんどん分割されていくのですが、実はこれが音楽と深いつながりがあるのです。僕はこのフィボナッチ格子と言われる原理を初めて知ったときに、即座にリズムとして叩いてみました。これを音楽的に解釈してみると、2拍子、3拍子、5拍=2.5拍子、8拍=2.666…拍子とすることができ、非整数拍子というものを定義できます。フィボナッチ数列は800年前から研究が重ねられていますが、この800年間、このようなかたちで音楽に利用されたという例をただの一つも知りません。逆に驚きを覚えてしまうのですが、それくらい異なった分野の概念は結びつきにくいものといえるでしょう。
このリズムは音楽だけでなく、階段の構造にも使えるはず、との確信から「民主主義的階段」という作品を制作しました。

この階段は登れば登るほど疲れがとれる階段です。といいますのも、スポーツにおいて整理体操というのは極度の疲れを解きほぐすために行うものですが、この階段の上り下りにおいて体感されるリズムも、心身のストレスを解きほぐすように作用するからです。少し大げさな言い方かもしれませんが、僕は数百年も経てば、この階段が世界標準になると思っています。このように階段と音楽は結びつくものなのです。階段とは音を使わない音楽のようなものだとも言えます。この階段、何も特殊な技術を用いているわけではありません。普通に階段をつくる技術に、ただ踏面の長短をフィボナッチ格子に当てはめて並べたものであり、アイデアだけが新しいのです。アイデアには重さが無く、消費されて減るわけでもありませんし、新しい工夫がなされたからといって余計なお金がかかるわけでもありません。

next

ページトップ△